
Modeling of a 4x10Gbps All-Optical Clock Extraction System
O.Frazão1, A.F.Cunha2, P.Tavares1, L.Ribeiro3, J.Ferreira da Rocha4
1
Institute of Telecommunications, Portugal, +351 34 383091, ofrazao@av.it.pt, ptavares@av.it.pt2
Dept. of Physics, University of Aveiro, Portugal, +351 34 370818, acunha@fis.ua.pt3
Dept. of Industrial Electronics, University of Minho, Portugal, +351 53 510190, lfbr@dei.uminho.pt4
Dept. of Electronics and Telecommunications, University of Aveiro, Portugal, +351 34 370200, frocha@ua.pt
Abstract
This paper reports a technical assessment of an all-optical 4x10Gbps clock extraction technique in the context of fiber optic digital communication systems. The technique consists in putting a 1320nm semiconductor laser in a self pulsating mode through injection locking to a CW source. The pulsations are triggered by a fast drive current step. The useful self pulsation region has been explored after extensive simulation providing a valuable knowledge for on-going experiments. Actual synchronization with optical data stream was observed both considering all ones and pseudo-random sequences. Phase sustaining of the clock over moderate-length sequences of zeros was noticed as the most encouraging result of this work.
1. Introduction
The research and development of optical networks is of interest worldwide for future interactive, flexible broadband communications services. In high bit rate network systems, time domain optical signal processing techniques such as optical time division multiplexing (OTDM), demultiplexing and time extraction are indispensable to overcome the electric processing speed limitations.
One important function in communications switching and transmission is synchronization. M. Jinno [1] demonstrated for the first time the use of self pulsating laser diode for all optical timing recovery. Barnsley [2] have also demonstrated optical timing recovery at 5Gbit/s in use in a 20Gbit/s optical time division multiplexed system. Mode-locking was used by Smith [3]. Two sections DFB laser was used by D.J.As [4] with dispersive self Q-switching for 18Gbps all optical clock extraction.
Timing extraction or clock recovery must produce a low jitter timing clock synchronized to the input optical signal because the extracted clock should be distributed to, for example, demultiplexers, routers, channel selectors and receivers.
In this work, optical clock recovery, using the injection locking mechanism, is investigated. Two single cavity DFB lasers, commercially available and operating at 1320nm, connected by fiber section tappers were used. The main goal is to produce a 10GHz optical clock signal suitable for demultiplexing a 4x10Gbps input data stream.
2. Theory
The conceptual model of the semiconductor LD with external light injection is illustrated in Fig.1. A coherent optical beam from an external source with frequency n is injected into the laser diode resonator through one of the facets.

Fig. 1 -
Diode laser model with external light injectionAccording to Lang [5], the injection locking mechanism is governed by the following set of coupled differential equations.
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
The first equation describes the electric field, E, behavior, where a is the cavity loss, G(n) represents the modal gain, w (n) is the resonant frequency of the cavity mode to which the light is injected, both are dependent on n, the carrier density. The electric field amplitude of the light coupled into the cavity, modified in such a way that it has units of (photons/m3)1/2, is represented by Eext. For the calculation, it is assumed that G(n) and w (n) are approximated by,
![]() (4)
(4)
![]() (5)
(5)
where g is the differential gain, W is the frequency of the light injected mode which has been assumed equal to the injected light frequency n and w th is the threshold cavity resonance frequency.
The possible excitation of the neighboring axial mode with detuning increase can be accounted for by the second equation for the photon density, S, in that mode. Parameter Csp is the spontaneous emission coefficient and t s is the carrier lifetime.
The last equation describes the excited carrier density, where P is the carrier injection rate per unit of volume.
In carrying out the numerical solution, it was convenient to define a new set of normalized variables [5]. The parameters are normalized with respect to cavity loss, a , equal to the inverse of photon lifetime.
Substitution of (4)-(5) into (1)-(3) yields, with the normalized variables, the following set of basic equations to describe the injection locking proprieties of a semiconductor laser.
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
In the above equations yo is the normalized electric field amplitude, x is the normalized carrier density, p is the normalized effective refractive index, d is the normalized detuning, q2 is the normalized injected power, zu is the normalized photon density in the neighboring axial mode, a is the normalized carrier lifetime, zo is the normalized intensity of the locked mode, r is the normalized relative excitation and T is the normalized time.
2. Analysis Results
The model above was used in the assessment of the instability region for a 1320nm semiconductor laser diode. This device has been characterized and its main features are summarized in table 1.
|
Name |
Description |
Value |
|
V |
Active layer volume |
1.0 x10-16 m3 |
|
t p |
Photon lifetime |
2 ps |
|
t s |
Carrier lifetime |
2 ns |
|
A |
Gain constant |
2 x10-20 m2 |
|
Ith |
Threshold current |
25mA |
|
h |
Refractive index |
3.5 |
|
h eff |
Effective refractive index |
3.8 |
|
G |
Confinement factor |
0.28 |
|
R |
R factor |
-2 |
|
Csp |
Spontaneous emission coefficient |
5.5 x10-5 |
Table 1 -
Laser diode parametersA constant photon density of Eext2 = 5.3 x1020 photons/m3 at the input of the active section was assumed.
2.1. Pulsation Conditions
We have studied the instability conditions in a single cavity semiconductor laser. This instability is originated in the laser when light is injected into it. This effect was studied by many researchers and is called injection locking. The influence of the external light injection level, detuning and increasing step height of excitation bias current was analyzed.
To achieve sustained laser pulsation it is necessary to induce the instability by a step increase of excitation bias current. The step must be applied after the laser steady state is reached at a bias current slight above threshold, that is Io» Ith. An approximate analytical expression for the locking range is given by [5],
![]() (6)
(6)
This equation basically relates the detuning and the relative excitation. In the simulations we have considered q2 = 7.9 x10-3.
It can be seen that the locking range decreases with 1/r1/2 for high relative excitation. Inside the locking range there are two really distinct regions, the stable and the unstable. According to Fig.2 the unstable range increases with the current step. This indicates that the clock extractor should be more stable for higher values of r. Within this locking range, however, on can achieve pulsed or CW output. The line separating this two outcomes was obtained through extensive simulations and can be seen in Fig. 2. The most interesting region for our study correspond to the locking range with pulsation
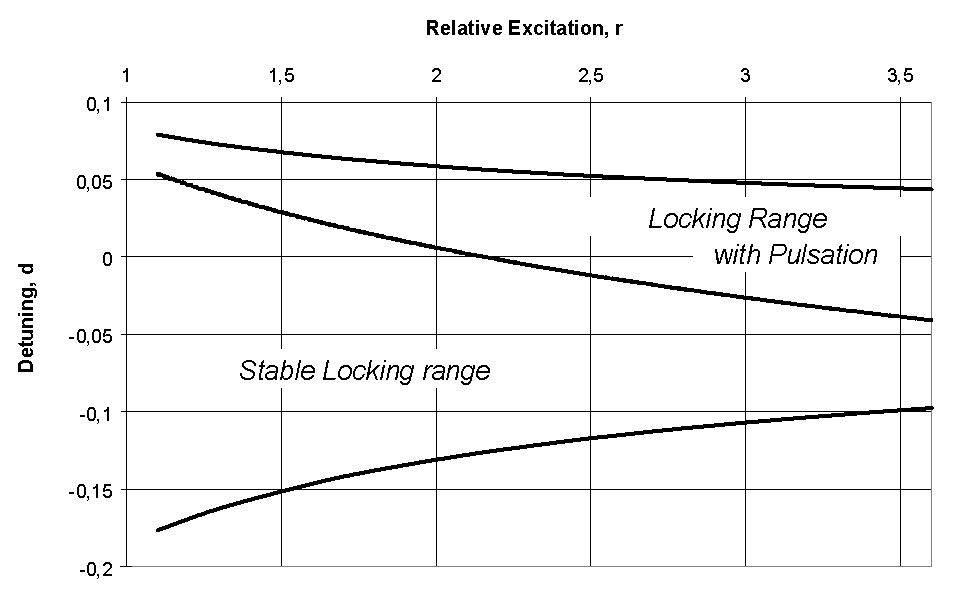
Fig. 2 -
Locking range dependence on the relative excitationIn Fig. 3 it can be seen that 10 GHz self sustained pulsation frequency, F , is achieved when the step is r = 3.4, which corresponds to an injected bias current of 110 mA and to an injection power of about q2 = 0.01, which corresponds to an optical power of 7.23mW for d=0.0. Below q=0.03 there are not sustained pulsation.
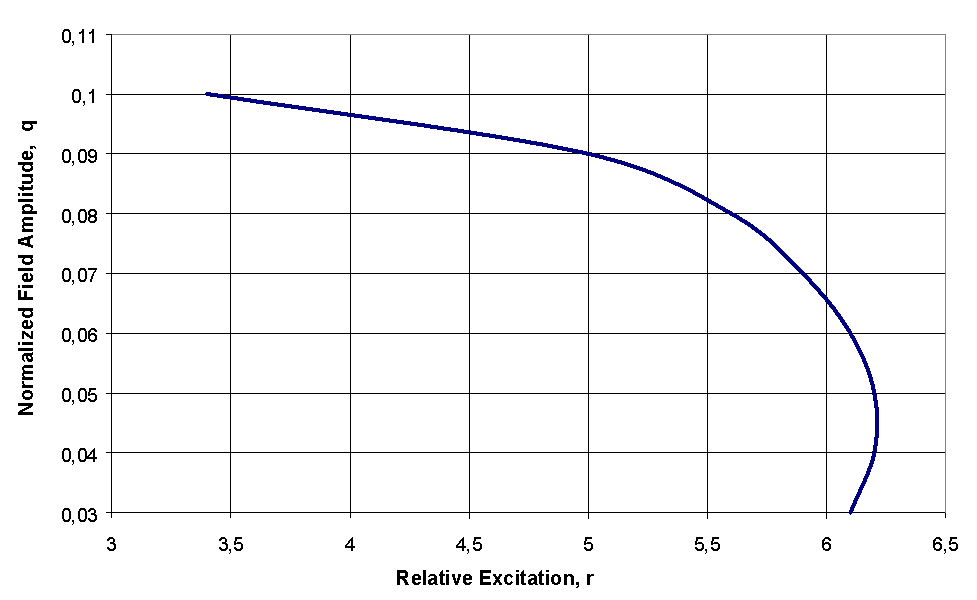
Fig. 3 -
Relationship between r and q for constant pulsation frequency 10 GHz.It was also found that 10 GHz can be achieved if the injected light level on the laser is reduced and the step increased significantly.
For a relative excitation of the order of 6, the laser will be driven at 175 mA. This value however is quite high for conventional semiconductor lasers. This means that a reasonable level of injected light must be guaranteed .
It was previously seen that 10GHz self-pulsation is achieved when the step is 3.2 and the detuning is 0.03 meaning that the injected light frequency is greater than the laser resonant frequency. In this case self-sustained pulsation has a ON-OFF behavior, see Fig. 4, which is of interest for our purposes.
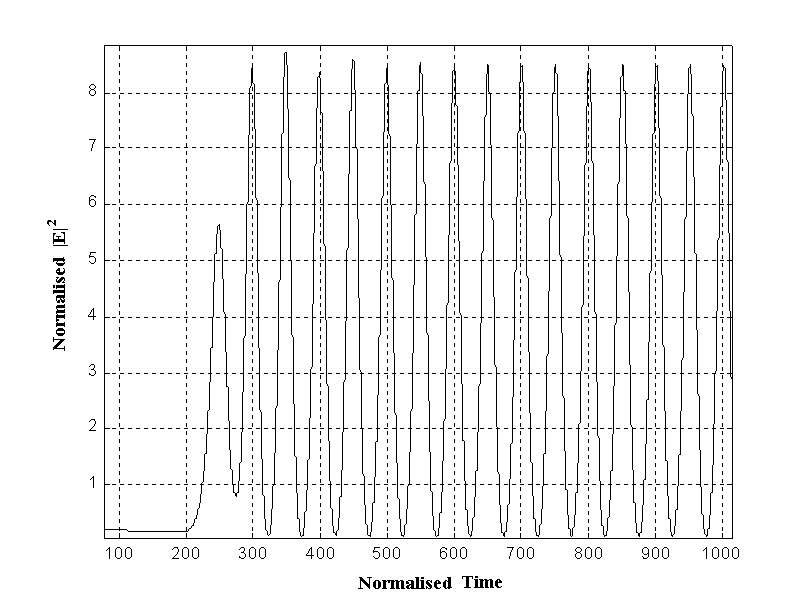
Fig. 4 -
Output response for d=0.03 and q = 0.089 to a step increase excitation current from r = 0.01 to r = 3.2 at T=200.
2.2. Synchronization and Clock Recovery
For the simulation of the clock extraction process, we have considered a 10Gbps data stream modulating in amplitude a 1320nm CW laser. The pulse format, as in soliton systems, is a RZ hyperbolic secant occupying approximately 1/4 of the bit time slot. The optical stream is combined with three delayed copies to generate a pseudo 40Gbps sequence as displayed in Fig. 5.
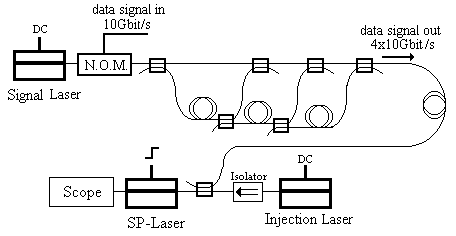
Fig. 5 -
All optical clock recovery simulated setup.Our goal is to produce a 10 GHz optical clock signal suitable to drive an optical demux. The solitons have 66.5m W peak to peak power and 5.2ps FWHM.
Self sustained pulsations near 10 GHz is a two level process. First thing to do is biasing the laser near threshold and injecting a optical power of about 7mW to reach the steady state. After that a step increase excitation current from near threshold to 105mA should be applied. It must be assured that detuning is inside the instability locking range. After we had achieved 10 GHz sustained pulsation an input data sequence is injected in the device at T=500. It was observed that the device adjusts its phase to the incoming data sequence as can be seen in Fig. 6.
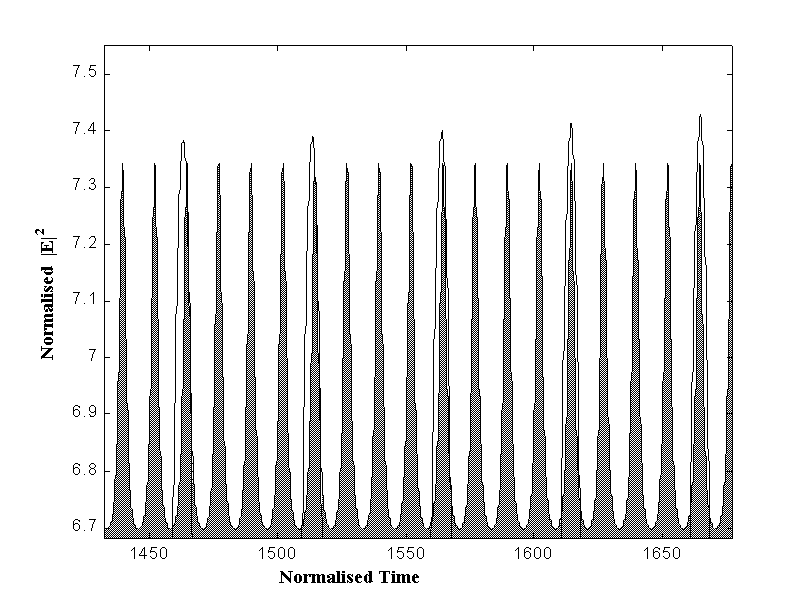
Fig. 6 -
Laser syncronization with an all ones input bit pattern.It is important to evaluate the system performance when the data stream in composed by randomly ordered 0s and 1s. The main aspect is the lock in range of the optical clock. This can be assessed looking at the phase drift dynamics when receiving long sequences of 0s. Good clock extractors should maintain phase for long times (typically 10 bit slots). In Fig. 7 is shown the response to actual data.
The phase synchronism is maintained if the pulsation frequency is very near to 10 GHz. There is a slightly amplitude modulation of the clock but we believe that this fact should not affect the demux functionality.
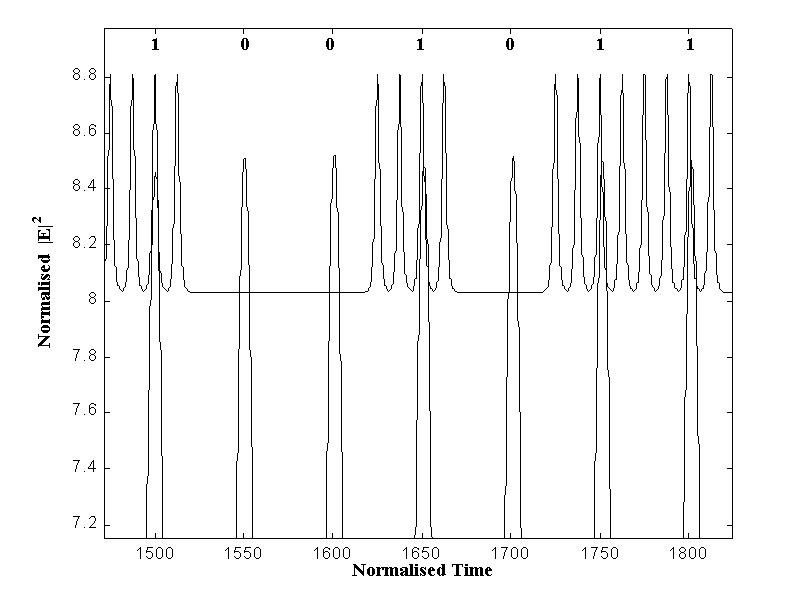
Fig. 7 -
Laser syncronization with an 1001011 input bit pattern input signal.The synchronization process has another consequence in terms of the output spectrum. In Fig. 8 we compare a free run device with an injection locked laser. We can see that narrowing of the locked spectra occurs.

Fig. 8 -
Output free run (b) and locked (a) spectra.3. Conclusions
From the simulations we conclude that the use of the injection locking mechanism can be used with success in all optical clock recovery.
It was seen that the clock extractor will be more stable for higher values of the relative excitation. However if the laser can not be driven with high currents than a reasonable level of injected light must be assured.
The phase synchronism can be guaranteed if the self pulsation frequency is near to 10 GHz.
Acknowledgments
This work is sponsored by the UPGRADE project from the ACTS (Advanced Communication Technologies and Services) program.
References
[1] M. Jinno, T.Matsumoto," Optical Retiming regenerator using 1.5 m m multi-electrode DFB LD,s", Electron. Letter., 1989, Vol. 25, pp.1332-1333.
[2] Barnsley, Wickens, Wckes and Spirit," A 4x5 Gbits transmission system with alll optical clock recovery" Photonics Technol. Lett. 1992,4,pp.83-86.
[3] K.Smith and J.K.Lucek, "All-optical clock recovery using a mode-locked laser", Electron. Letter., 1992, Vol 28, pp.1814-1816.
[4] D.J.As and U.Feiste, "Clock recovery based on a new type of self pulsation in a 1.5 m m two-section InGaAsP/InP DFB Laser", Electron. Letter., 1992, Vol 29, pp.141-142.
[5] Roy Lang, "Injection Locking Proprieties of a Semiconductor Laser", IEEE Journal of Quantum Electronics, Vol. QE-18, Nş6, pp. 976-983, June 1982.